非空真子集：集合论中的重要概念及计算方法

非空子集的定义与计算

在集合论中，非空子集是一个重要的概念。它指的是一个集合的所有子集中，不包括空集的子集。空集是只包含一个元素，即什么都不包含的集合，记作∅。而任何非空集合的真子集都不可能是空集，因此非空子集必然是除去空集之外的子集。

非空子集的个数可以通过公式2^n-1来计算，其中n是集合中的元素个数。这是因为一个包含n个元素的集合有2^n个子集，包括空集和自身。从中减去空集，就得到了非空子集的个数。

1、真子集也是集合的一个重要概念。如果集合A是集合B的子集，但A≠B，那么我们说A是B的真子集。真子集必然是非空子集，但反之则不一定成立。

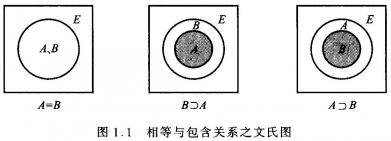
对于一个包含n个元素的集合，它的真子集个数为2^n-1，而非空真子集的个数为2^n-2。这是因为真子集中包括了一个空集，所以要减去一个。

非空子集是集合的一个重要属性，它的个数可以通过公式2^n-1来计算。同时，真子集和非空真子集也是集合论中的重要概念，它们之间的关系和计算方法也需要我们深入理解。