余弦函数：邻边与斜边的比值

余弦函数及其应用

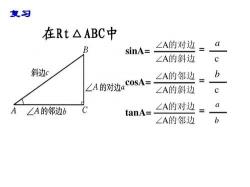
余弦函数是三角函数的一种，定义为邻边与斜边的比值。在直角三角形ABC中，角C为90度，角A的余弦即为邻边b与斜边c的比值，即cosA=b/c，也可以表示为cosa=AC/AB。除此之外，余弦函数f(x)=cosx的定义域为全体实数。

在进行三角函数求解时，我们需要用到两根判别法。该方法中，我们记m(c1,c2)为c的两值为正根的个数，c1为c的表达式中根号前取加号的值，c2为c的表达式中根号前取减号的值。具体判别方式如下：

若m(c1,c2)=2，则有两解。

若m(c1,c2)=1，则有一解。

若m(c1,c2)=0，则有零解（即无解）。

同时需要注意，若c1等于c2且c1或c2大于0，此种情况算到第二种情况，即一解。

角边判别法也是求解三角函数的重要方法。具体如下：

当a>bsinA时：

(1) 当b>a且cosA>0（即A为锐角）时，则有两解；

(2) 当b>a且cosA≤0（即A为直角或钝角）时，则有零解（即无解）；

(3) 当b=a且cosA>0（即A为锐角）时，则有一解；

(4) 当b=a且cosA≤0（即A为直角或钝角）时，则有零解（即无解）；

(5) 当b<a时，则有一解。

当a=bsinA时：

(1) 当cosA>0（即A为锐角）时，则有一解；

(2) 当cosA≤0（即A为直角或钝角）时，则有零解（即无解）。

当a<bsinA时，则有零解（即无解）。