一次函数知识点总结：定义、解析式、图像与性质全面解析

一、一次函数的定义

一般地，形如y=kx＋b(k，b是常数，且k≠0)的函数，叫做一次函数，其中x是自变量。当b=0时，一次函数y=kx，又叫做正比例函数。

二、一次函数的解析式

一次函数的解析式的形式是y=kx＋b，要判断一个函数是否是一次函数，就是判断是否能化成以上形式。

三、正比例函数与一次函数的关系

正比例函数是一次函数的特例，一次函数包括正比例函数。

四、一次函数的图像及性质

在一次函数上的任意一点P(x，y)，都满足等式：y=kx+b。

一次函数与y轴交点的坐标总是(0，b)，与x轴总是交于(-b/k，0)。

正比例函数的图像总是过原点。

k，b与函数图像所在象限的关系：当k>0时，y随x的增大而增大；当k<0时，y随x的增大而减小。

五、一次函数的图象与性质的口诀

一次函数是直线，图象经过三象限；正比例函数更简单，经过原点一直线；两个系数k与b，作用之大莫小看，k是斜率定夹角，b与y轴来相见，k为正来右上斜，x增减y增减；k为负来左下展，变化规律正相反；k的绝对值越大，线离横轴就越远。

六、一次函数应用常用公式

求函数图像的k值：（y1-y2)/(x1-x2)

求与x轴平行线段的中点：(x1+x2)/2

求与y轴平行线段的中点：(y1+y2)/2

求任意线段的长：√[(x1-x2)2+(y1-y2)2]

求两个一次函数式图像交点坐标：解两函数式

求任意2点所连线段的中点坐标：[（x1+x2）/2，（y1+y2）/2]

求任意2点的连线的一次函数解析式：（x-x1）/(x1-x2)=(y-y1)/(y1-y2)

若两条直线y1=k1x+b1//y2=k2x+b2，则k1=k2，b1≠b2

如两条直线y1=k1x+b1⊥y2=k2x+b2，则k1×k2=-1

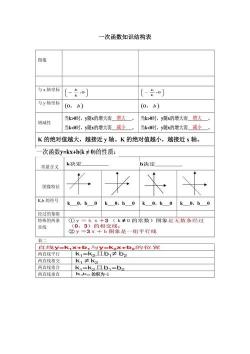
y=k（x-n）+b就是直线向右平移n个单位

y=k（x+n）+b就是直线向左平移n个单位

y=kx+b+n就是向上平移n个单位

y=kx+b-n就是向下平移n个单位

口决：左加右减相对于x，上加下减相对于b。

七、直线与坐标轴的交点

直线y=kx+b与x轴的交点：(-b/k，0)与y轴的交点：(0，b)