理解互质数：数学中的独特关系

一、引言

互质数，数学中的一个重要概念，涉及到两个或多个整数的公因数。当这些整数的公因数只有1时，它们被称为互质数。本文将深入探讨互质数的定义、定理以及判断方法。

二、互质数的定义

互质数，也称为相对质数，是指在数学中，两个或多个整数的公因数只有1的非零自然数。换句话说，公因数只有1的两个非零自然数被称为互质数。需要注意的是，“两个数”是指除0外的所有自然数，并且“公因数只有1”不能误说成“没有公因数”。

三、互质数的定理

互质数具有以下定理：

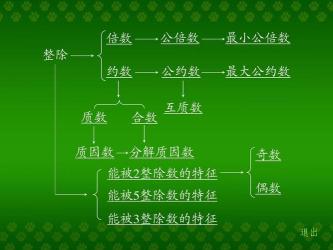
两个不同的质数一定是互质数。例如，2和3只有1作为公因数，因此它们是互质数。

1和任何自然数互质。例如，1和17只有1作为公因数，所以它们是互质数。

两个数中的较大一个是质数，这两个数一定是互质数。例如，3和19是互质数，因为19是一个质数。

两个整数（正整数）（N），除了1以外，没有其他公约数时，称这两个数为互质数。互质的两个数相乘，所得的数不一定是合数。

四、互质数的判断方法

正确、快速地判断两个数是不是互质数对于求两个数的最大公约数和最小公倍数起着关键作用。以下是几种判断方法：

概念判断法：根据互质数的定义，如果两个数的公约数只有1，则它们是互质数。例如，9和11只有1作为公约数，因此它们是互质数。

规律判断法：利用一些已知的互质数规律进行判断。例如，两个连续的自然数一定是互质数（如4和5），或者相邻的两个奇数一定是互质数（如5和7）。

分解判断法：如果两个数都是合数，可先将它们分别分解质因数，然后查看是否含有相同的质因数。如果没有相同的质因数，这两个数是互质数。例如，130和231分解后没有相同的质因数，因此它们是互质数。

求差判断法：适用于两个相差不大的数。先求出两数的差，然后查看差与其中较小数是否互质。如果互质，则原来两个数是互质数。例如，194和201的差是7，7与194互质，所以194和201是互质数。

求商判断法：用大数除以小数，观察除得的余数与其中较小数是否互质。如果余数与较小数互质，则原来两个数是互质数。例如，317除以52的余数是5，5与52互质，因此317和52是互质数。

五、结语

通过对互质数的深入探讨，我们可以更好地理解这一概念在数学中的应用。掌握互质数的定义、定理以及判断方法对于解决涉及最大公约数和最小公倍数的问题具有重要意义。在实际应用中，我们可以根据具体情况选择合适的判断方法来快速准确地确定两个数是否为互质数。