幂函数的性质及其在不同参数下的表现

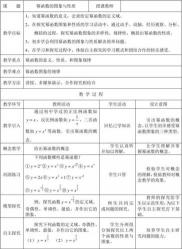
幂函数的性质

当α>0时，幂函数y=x^α具有以下性质：

图像通过点(1,1)和(0,0)；

在区间[0, +∞)上为增函数；

在第一象限内，α>1时，导数值逐渐增大，α=1时，导数为常数，0<α<1时，导数值逐渐减小并趋近于0。

当α<0时，幂函数y=x^α具有以下性质：

图像通过点(1,1)；

在区间(0, +∞)上为减函数；

若函数为偶函数如X-2，利用对称性可知其在区间(-∞,0)上单调递增；

在第一象限内，有两条渐近线（即坐标轴），自变量趋近0时，函数值趋近+∞，自变量趋近+∞时，函数值趋近0。

当α=0时，幂函数y=x^α具有以下性质：

y=x^0的图像是直线y=1去掉一点(0,1)，并非是一条直线。